Improving weather and climate forecasts

15 August 2014

Dr. Eike Mueller and Prof. Rob Scheichl of the Department of Mathematical Sciences at the University of Bath use the Emerald GPU-accelerated supercomputer to develop highly scalable iterative solvers for very large partial differential equations in numerical weather and climate prediction.

Overview

To improve the accuracy of numerical weather and climate prediction codes, the model resolution has to be continuously increased. At the same time the total run-time has to satisfy strict operational requirements: tomorrow’s forecast is not very useful if it takes a week to produce it! This requires the development of highly scalable numerical algorithms which can run efficiently on modern computer architectures such as GPUs.

One of the key ingredients in many atmospheric models, such as the Met Office Unified Model, is a solver for an elliptic partial differential equation (PDE) for the pressure correction. This equation has to be solved at every model time step and is one of the computational bottlenecks of a model run. If the global resolution is increased to 1km, this equation has around 1011
unknowns and can only be solved with algorithmically efficient and highly parallel solvers. As the PDE is discretised in a thin spherical shell representing the earth’s atmosphere, it is strongly anisotropic and this has to be taken into account when designing a good solver; equations with a very similar structure arise in many other fields of geophysical modelling such as subsurface flow simulations (see e.g. Lacroix (2003)) or global ocean and ice sheet models . The ideas and results developed in this project therefore have a wide range of applications both in academic research and in industry

Eike Mueller and Rob Scheichl developed an algorithmically optimal geometric multigrid solver which can handle the strong vertical anisotropy. They implemented and optimised it in the CUDA-C framework and tested its performance and parallel scalability on up to 100 GPUs of the EMERALD cluster.

Challenges

The main challenge of sparse iterative solver algorithms is the limited global memory bandwidth of modern GPUs: on EMERALD’s Fermi M2090 cards around 30 floating point operations can be carried out in the time it takes to read one variable from memory. For this reason implementing the algorithm in a way which minimises global memory access is crucial to reduce the total solution time. For problems with billions of unknowns, multiple GPUs have to be used simultaneously, and they have to continuously exchange data to produce a consistent solution. It is important to use a communication library which minimises transfer time by exploiting techniques such as GPUDirect. This is particularly important on the coarser multi gridlevels where the ratio between calculations and communication is less favourable.

Solution

Eike Mueller and Rob Scheichl designed an algorithmically optimal geometric algorithm based on the tensor product idea in Boerm and Hiptmair (2001). In contrast to algebraic multigrid codes this allows a matrix-free implementation in which the local matrix stencil is recalculated instead of reading it from GPU memory. This has a significant impact on the performance and reduces storage requirements dramatically. In addition they exploited the structure of the equation to minimise the work carried out on the coarse multigrid levels which suffer from a poor communication-to-calculation ratio. Fusion of computational kernels allowed better cache-reuse and further reduces expensive reads from global GPU memory. To achieve fast communication over the network, the multi-GPU implementation was based on the Generic Communication Library (GCL) developed at CSCS in Switzerland (see Bianco et al. (2014)). This Library can be used to implement halo-exchanges on structured grid, it uses GPUDirect to minimise communication times between different GPUs.

As the ultimate goal of the project is the development of a massively parallel solver, it was crucial to test the code on a large number of GPUs to assess it’s performance and parallel scalability. The EMERALD cluster is the only national resource which could be used to carry out these tests. With the support of SES, Eike Mueller and Rob Scheichl were able to use a sizeable fraction of the machine and run tests on up to 100 GPUs. Support from SES was also important during code development.

Key results

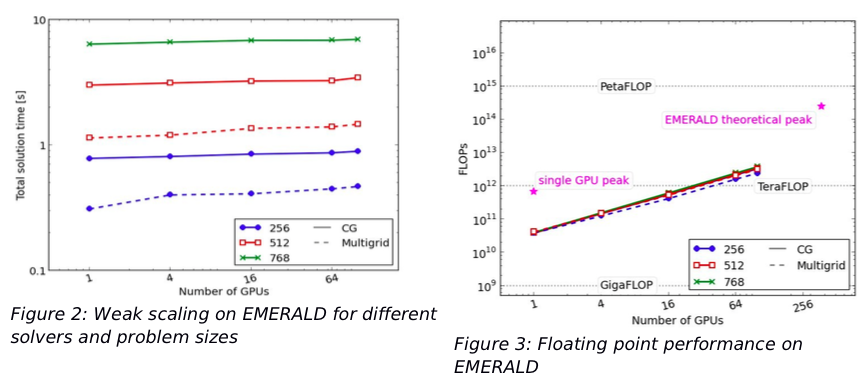
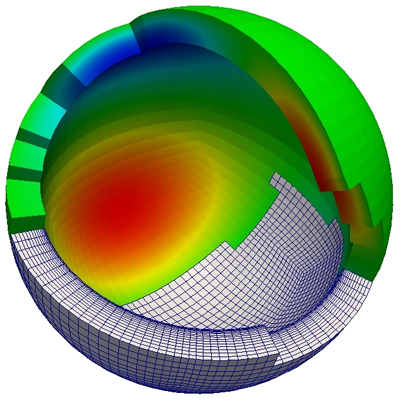
Both a Conjugate Gradient and the matrix-free multigrid solver were tested for different problem sizes and on several GPUs. On a single GPU the code could achieve a floating point performance of up to 42 GFLOPS/s (6% of theoretical peak). As the code is limited by the memory bandwidth, a more meaningful performance indicator is the utilised global memory bandwidth. Here the code could use between 30% and 50% of the theoretical peak value, which is a sizeable fraction for a memory bound algorithm. Excellent weak scaling was achieved on up to 100 GPUs, the multigrid solver was able to solve a problem with 3 billion (3×109) unknowns in less than 2 seconds, while reducing the residual by five orders of magnitude. More details on this work can be found in Mueller et al. (2015).

Based on research described in the case study, multigrid solvers have recently been implemented in the Met Office climate and weather forecasting codes. One of these solvers is currently used for operational forecasts, and has led to a significant reduction in model runtime, as described in this article. In addition, multigrid is used in the Met Office’s next generation model, which is expected to become the main numerical forecast model around 2026 (Maynard et al. (2020)).

Contact

Dr Eike Müller

Senior Lecturer, University of Bath

Open twitter profile

• Energy and climate change
• climate change